La lámpara incandescente se inventó en 1870. La primera lámpara consistía en un filamento de carbón contenida en un recipiente de vidrio en el que se había hecho el vacío. Esta lámpara duraba muy poco y fue sustituida por lámparas de filamento metálico, principalmente de volframio.
La lámpara incandescente funciona cuando un filamento metálico se calienta a altas temperaturas. Los electrones de los átomos emiten energía en todas las longitudes de onda. Cuando una parte importante de la radiación emitida está en el espectro visible y podemos ver el objeto por la radiación visible que emite, decimos que está incandescente.
Para que un sólido emita radiación visible tiene que estar a una temperatura de 850 K, entonces lo vemos de color rojo. Comparando con la temperatura de 6500 K de la fotosfera solar, podemos afirmar que es imposible conseguir calentar un objeto sólido a esta temperatura sin que se funda, para que emita el mismo espectro de la radiación que el Sol.
El volframio es el metal que tiene a la vez la temperatura más alta de fusión 3680 K y el menor grado de evaporación. El carbono soporta temperaturas más elevadas antes de fundirse pero se evapora rápidamente.
En la práctica, la temperatura más alta que soporta una lámpara incandescente ordinaria fabricada con filamento de volframio es de 2900 K. A estas temperaturas solamente, una pequeña fracción de de la energía emitida está en la región visible, menos del 11%, la mayor parte de es radiación infrarroja. Por lo que las lámparas incandescentes son poco eficientes en la emisión de luz visible.
Hemos supuesto que el filamento se comporta como un cuerpo negro, ignorando la emisividad ε que depende la temperatura y de la longitud de onda y el coeficiente de transmisión del vidrio de la lámpara. Por ejemplo, la emisividad del volframio a la longitud de onda de 0.65·10-6 m (color rojo) y al la temperatura de 2900 K es deε=0.420.
Actividades
En el applet situado al final de la
página anterior
Se introduce
- la temperatura (K), en el control de edición titulado Temperatura
- Elegir en el control de selección titulado Región del espectro, el elemento visible.
Se pulsa el botón titulado
Calcular.
Anotar la proporción de la energía emitida por unidad de área y unidad de tiempo en esta región del espectro por un cuerpo negro calentado a esta temperatura.
En la
página siguiente se explicará como se determina la temperatura del filamento de una lámpara incandescente a partir de la medida de su resistencia.
Para determinar la temperatura de la radiación de un cuerpo negro o de una estrella de la misma temperatura se mide la longitud de onda
λm a la cual el cuerpo negro emite con intensidad máxima. Aplicando la ley de Wien
λm ·T=2.898·10-3 m·K
se determina la temperatura de dicho cuerpo. Por ejemplo, si el máximo está en la longitud de onda λm=0.5·10-6 m, la temperatura del cuerpo negro es de 5800 K, tal como se muestra en la figura.
 La radiación Sol es absorbida por la atmósfera de la Tierra, por lo que no es fácil determinar la longitud de onda a la cual se produce la máxima intensidad.
Otra forma de medir la temperatura del Sol, es la aplicación de la ley de Stefan-Boltzmann. La energía emitida por unidad de tiempo en todo el espectro por un cuerpo negro a la temperatura T es
P=σAT4
La radiación Sol es absorbida por la atmósfera de la Tierra, por lo que no es fácil determinar la longitud de onda a la cual se produce la máxima intensidad.
Otra forma de medir la temperatura del Sol, es la aplicación de la ley de Stefan-Boltzmann. La energía emitida por unidad de tiempo en todo el espectro por un cuerpo negro a la temperatura T es
P=σAT4
donde
A es el área de la superficie del cuerpo. La temperatura
T efectiva del Sol será la de un cuerpo negro de la misma área
A que emita la energía
P por unidad de tiempo del Sol.
Supongamos que el Sol es una esfera de radio
R, y que medimos la intensidad de la radiación solar a una distancia
rdel centro del Sol, por ejemplo en la Tierra.
La energía emitida por el Sol, supuesto un cuerpo negro a la temperatura
T es
P=4π
R2σT4
Si suponemos que el Sol emite en todas las direcciones de forma isótropa. La intensidad de la radicación solar a una distancia
r del centro del Sol es

 | Datos:
- Constante de Stefan-Boltzmann s =5.67·10-8 (Wm-2K-4).
- Radio del Sol, R=6.96·108 m
- Distancia entre la Tierra y el Sol, r=1.49·1011 m.
- Intensidad de la radiación solar medida en la órbita de la Tierra I=1390 W/m2
|
Lo que nos da una temperatura
T=5790 K.
 | Supongamos un pequeño cuerpo esférico de radio r, suspendido en el interior de una gran cavidad en la que se ha hecho el vacío y cuyas paredes se encuentran a la temperatura T0. Si la temperatura inicial de la bola esférica es T al cabo de un cierto tiempo, se habrá alcanzado el equilibrio en el que la temperatura de la esfera será la misma que la de las paredes de la cavidad. |
Como hemos visto al estudiar las propiedades de la
superficie de un cuerpo, el valor del coeficiente de absorción
aestá comprendido entre 0 (para un reflector perfecto) y 1 (para una superficie idealmente negra). En vez de
a, se suele emplear la denominada emitancia relativa
e de la superficie que es numéricamente igual a
a.
- Energía radiante emitida por el pequeño cuerpo
La cantidad de energía radiante emitida por unidad de área y por unidad de tiempo desde la superficie de un cuerpo a temperatura T, viene dada por la expresión

La ley de Stefan-Boltzmann es también válida para cualquier otro cuerpo (gris) cuya superficie tenga un coeficiente de absorción (o emitancia) independiente de la longitud de onda.
Multiplicando por el área de la superficie del pequeño cuerpo, obtenemos la energía Pe que pierde el cuerpo en la unidad de tiempo debido a la emisión de la radiación.

- Energía radiante absorbida por el cuerpo
También incide energía radiante sobre la superficie del cuerpo. Una parte de la energía incidente es absorbida Pa que se obtiene multiplicando la intensidad de la radiación por el área de su superficie, por la fracción a de la energía incidente que es absorbida. Como hemos dicho, este factor a es numéricamente igual a e.

- Variación en la temperatura del cuerpo con el tiempo
La cantidad de energía neta por unidad de tiempo (perdida o ganada) es igual a la diferencia entre la energía radiante absorbida y la emitida .

La cantidad de energía radiante ganada (perdida) se emplea en aumentar (disminuir) la temperatura del cuerpo. Si la masa del cuerpo es m, y su calor específico del cuerpo es cv, escribimos

La temperatura del cuerpo varía con el tiempo hasta que se establece el equilibrio térmico a la temperaturaT0 de las paredes de la cavidad.

donde hemos sustituido la masa m por el producto de la densidad r por el volumen de la pequeña esfera de radio r.
Actividades
El programa interactivo, nos permite investigar los factores de los que depende el tiempo que tarda una bolita de radio
r, densidad
r , calor específico
cv, y emisividad
e, en alcanzar el equilibrio térmico con una cavidad grande cuyas paredes se mantienen una temperatura constante
T0.
Investigaremos con cuatro materiales cuyas propiedades se proporcionan en la siguiente tabla
| | Densidad kg/m3 | Calor específico J/(kg·K) |
| Hierro |
7880
|
450
|
| Aluminio |
2700
|
880
|
| Plomo |
11350
|
130
|
| Sodio |
975
|
1300
|
Se elige el material, en el control de selección
Material.
Se introduce
- la emitancia, un número entre 0 y 1, en el control de edición titulado Emitancia.
- la Temperatura de las paredes de la cavidad en grados centígrados.
- la Temperatura inicial del cuerpo en grados centígrados.
- el radio de la bolita se ha fijado en 10 cm.
Se pulsa en el botón titulado
Empieza.
Se representa la temperatura del cuerpo en función del tiempo. En el eje vertical se mide la temperatura en grados centígrados, y en el eje horizontal se mide el tiempo en minutos.
A la izquierda del applet se representa la intensidad de la radiación emitida por la esfera (en color rojo) y la intensidad de la radiación absorbida por el pequeño cuerpo (en color azul). La primera es proporcional a la cuarta potencia de la temperatura absoluta del cuerpo (cambia con dicha temperatura) y la segunda, es proporcional a la cuarta potencia de la temperatura absoluta de la cavidad (no se modifica).
El cuerpo aumenta su temperatura cuando la cantidad de energía absorbida en la unidad de tiempo es superior a la emitida, y disminuye su temperatura cuando la cantidad de energía emitida en la unidad de tiempo es superior a la absorbida. Cuando se alcanza la situación de equilibrio, ambas cantidades son iguales.

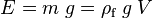


 aplicada en un punto P con respecto de un punto O viene dado por el
aplicada en un punto P con respecto de un punto O viene dado por el  por el vector
por el vector 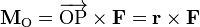
 es el vector que va desde O a P. Por la propia definición del
es el vector que va desde O a P. Por la propia definición del  es un vector perpendicular al plano determinado por los vectores
es un vector perpendicular al plano determinado por los vectores  y
y 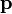 , y el
, y el , definido como
, definido como


