Leyes de Newton Las leyes de Newton, también conocidas como leyes del movimiento de Newton, son tres principios a partir de los cuales se explican la mayor parte de los problemas planteados por la mecánica, en particular aquellos relativos al movimiento de los cuerpos, que revolucionaron los conceptos básicos de la física y el movimiento de los cuerpos en el universo.
Constituyen los cimientos no solo de la dinámica clásica sino también de lafísica clásica en general. Aunque incluyen ciertas definiciones y en cierto sentido pueden verse como axiomas, Newton afirmó que estaban basadas en observaciones y experimentos cuantitativos; ciertamente no pueden derivarse a partir de otras relaciones más básicas. La demostración de su validez radica en sus predicciones... La validez de esas predicciones fue verificada en todos y cada uno de los casos durante más de dos siglos.2
En concreto, la relevancia de estas leyes radica en dos aspectos: por un lado constituyen, junto con la transformación de Galileo, la base de la mecánica clásica, y por otro, al combinar estas leyes con la ley de la gravitación universal, se pueden deducir y explicar las leyes de Kepler sobre el movimiento planetario. Así, las leyes de Newton permiten explicar, por ejemplo, tanto el movimiento de los astros como los movimientos de los proyectiles artificiales creados por el ser humano y toda la mecánica de funcionamiento de las máquinas. Su formulación matemática fue publicada por Isaac Newton en 1687 en su obra Philosophiae naturalis principia mathematica.nota 1
La dinámica de Newton, también llamada dinámica clásica, solo se cumple en los sistemas de referencia inerciales (que se mueven a velocidad constante; la Tierra, aunque gire y rote, se trata como tal a efectos de muchos experimentos prácticos). Solo es aplicable a cuerpos cuya velocidad dista considerablemente de la velocidad de la luz; cuando la velocidad del cuerpo se va aproximando a los 300 000 km/s (lo que ocurriría en los sistemas de referencia no-inerciales) aparecen una serie de fenómenos denominados efectos relativistas. El estudio de estos efectos (aumento de la masa y contracción de la longitud, fundamentalmente) corresponde a la teoría de la relatividad especial, enunciada por Albert Einstein en 1905.
Constituyen los cimientos no solo de la dinámica clásica sino también de lafísica clásica en general. Aunque incluyen ciertas definiciones y en cierto sentido pueden verse como axiomas, Newton afirmó que estaban basadas en observaciones y experimentos cuantitativos; ciertamente no pueden derivarse a partir de otras relaciones más básicas. La demostración de su validez radica en sus predicciones... La validez de esas predicciones fue verificada en todos y cada uno de los casos durante más de dos siglos.2
En concreto, la relevancia de estas leyes radica en dos aspectos: por un lado constituyen, junto con la transformación de Galileo, la base de la mecánica clásica, y por otro, al combinar estas leyes con la ley de la gravitación universal, se pueden deducir y explicar las leyes de Kepler sobre el movimiento planetario. Así, las leyes de Newton permiten explicar, por ejemplo, tanto el movimiento de los astros como los movimientos de los proyectiles artificiales creados por el ser humano y toda la mecánica de funcionamiento de las máquinas. Su formulación matemática fue publicada por Isaac Newton en 1687 en su obra Philosophiae naturalis principia mathematica.nota 1
La dinámica de Newton, también llamada dinámica clásica, solo se cumple en los sistemas de referencia inerciales (que se mueven a velocidad constante; la Tierra, aunque gire y rote, se trata como tal a efectos de muchos experimentos prácticos). Solo es aplicable a cuerpos cuya velocidad dista considerablemente de la velocidad de la luz; cuando la velocidad del cuerpo se va aproximando a los 300 000 km/s (lo que ocurriría en los sistemas de referencia no-inerciales) aparecen una serie de fenómenos denominados efectos relativistas. El estudio de estos efectos (aumento de la masa y contracción de la longitud, fundamentalmente) corresponde a la teoría de la relatividad especial, enunciada por Albert Einstein en 1905.
Momento de fuerza
En mecánica newtoniana, se denomina momento de una fuerza (respecto a un punto dado) a una magnitud(pseudo)vectorial, obtenida como producto vectorial del vector de posición del punto de aplicación de la fuerza (con respecto al punto al cual se toma el momento) por el vector fuerza, en ese orden. También se denomina momento dinámico o sencillamente momento.
Ocasionalmente recibe el nombre de torque a partir del término inglés (torque), derivado a su vez del latín torquere(retorcer).
El momento de una fuerza  aplicada en un punto P con respecto de un punto O viene dado por el producto vectorial del vector
aplicada en un punto P con respecto de un punto O viene dado por el producto vectorial del vector  por el vector fuerza; esto es,
por el vector fuerza; esto es,
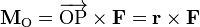
Donde  es el vector que va desde O a P. Por la propia definición del producto vectorial, el momento
es el vector que va desde O a P. Por la propia definición del producto vectorial, el momento  es un vector perpendicular al plano determinado por los vectores
es un vector perpendicular al plano determinado por los vectores  y
y  .
El término momento se aplica a otras magnitudes vectoriales como el momento lineal o cantidad de movimiento
.
El término momento se aplica a otras magnitudes vectoriales como el momento lineal o cantidad de movimiento 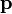 , y elmomento angular o cinético,
, y elmomento angular o cinético,  , definido como
, definido como

En mecánica newtoniana, se denomina momento de una fuerza (respecto a un punto dado) a una magnitud(pseudo)vectorial, obtenida como producto vectorial del vector de posición del punto de aplicación de la fuerza (con respecto al punto al cual se toma el momento) por el vector fuerza, en ese orden. También se denomina momento dinámico o sencillamente momento.
Ocasionalmente recibe el nombre de torque a partir del término inglés (torque), derivado a su vez del latín torquere(retorcer).
El momento de una fuerza  aplicada en un punto P con respecto de un punto O viene dado por el producto vectorial del vector
aplicada en un punto P con respecto de un punto O viene dado por el producto vectorial del vector  por el vector fuerza; esto es,
por el vector fuerza; esto es,
 aplicada en un punto P con respecto de un punto O viene dado por el producto vectorial del vector
aplicada en un punto P con respecto de un punto O viene dado por el producto vectorial del vector  por el vector fuerza; esto es,
por el vector fuerza; esto es,
Donde  es el vector que va desde O a P. Por la propia definición del producto vectorial, el momento
es el vector que va desde O a P. Por la propia definición del producto vectorial, el momento  es un vector perpendicular al plano determinado por los vectores
es un vector perpendicular al plano determinado por los vectores  y
y  .
.
 es el vector que va desde O a P. Por la propia definición del producto vectorial, el momento
es el vector que va desde O a P. Por la propia definición del producto vectorial, el momento  es un vector perpendicular al plano determinado por los vectores
es un vector perpendicular al plano determinado por los vectores  y
y  .
.
El término momento se aplica a otras magnitudes vectoriales como el momento lineal o cantidad de movimiento 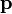 , y elmomento angular o cinético,
, y elmomento angular o cinético,  , definido como
, definido como
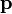 , y elmomento angular o cinético,
, y elmomento angular o cinético,  , definido como
, definido como
No hay comentarios:
Publicar un comentario